2024. 8. 9. 14:56ㆍ기계 학습 (Machine Learning)/수학 (Mathematics)

Variance
우리가 어렸을 때
정말 빠짐없고 아낌없이 배웠던
통계 지식 두 가지는 바로 평균(mean)과 분산(variance)입니다.
여기서 평균은 우리가 일생을 살아오면서
많이 보고, 사용했었지만서도
분산은 그 당시에서도 그랬고 지금도 그렇고
현실을 살아가면서 그다지 필요성을 느끼지 못했죠.
하지만 의외로 분산은 우리 삶에서 뗄레야 뗄 수 없는 요소입니다.
평균은 숫자들의 대표를 선출한다고 하면,
분산은 숫자들의 위치를 알려주기 때문입니다.
예를 들어 우리가 차를 타고 출근하려고 할 때,
어제 점심때는 막히지 않았던 길이
오늘 아침에서는 막혀서 답답했던 적이 있을 것입니다.

이때 우리는 핸들을 쿵치며 생각하죠.
이렇게 도로에서 시간 버리고 답답해할 바에는,
다른 시간을 고르거나 다른 길을 찾아보겠다고...
이때 우리의 머리 속에서는
죽기 살기로 분산을 계산하려고 합니다.
즉, 우리는 차가 없는 시간대 또는 장소를 찾아보고, 생각하게 됩니다.
동일 장소에서 시간대별로 출근 차량 개수를 세보거나
같은 시간에서 장소별로 출근 차량 개수를 세보겠죠.
출근시간의 격차가 다들 고만고만하게 비슷하면
뭐... 그냥 가던길로 가야지 하겠고
격차가 심하다고 하면 더 뚫린 길로 결정할 것입니다.
이렇게 분산은 어차피 모두가 겪는 일인데,
보통 우리가 분산이 짜증난다고 말하는 이유는
분산을 계산하는 수식만 보고
위치라는 의미를 가늠하기 어렵기 때문입니다.

분산(v)는 숫자 1개에 불과합니다.
대부분은 이 숫자 하나에 죽어라 의미를 부여하고,
오른쪽 계산식은 그저 숫자를 구하는 계산으로만 인식하고 있습니다.
하지만 아닙니다.
분산은 떡하니 나오지 않죠.
이를 구하기 위해서는 각 분포를 어떻게든 구해야 합니다.
예를 들어 오전 9시의 차량 현황을 조사했다고 해봅시다.

조사 결과, 각 길마다 차량 통행량이 차이가 심합니다.
이 경우에 분산이 크지만, 이건 중요한 게 아닙니다.
우리가 모든 길에 대해서 '차량 통행량'을 알고 있고,
우리 삶에 도움이 되는 의사 결정을 내릴 수 있다는 게 중요하죠.
한 번 오후 2시의 차량 통행량을 볼까요?
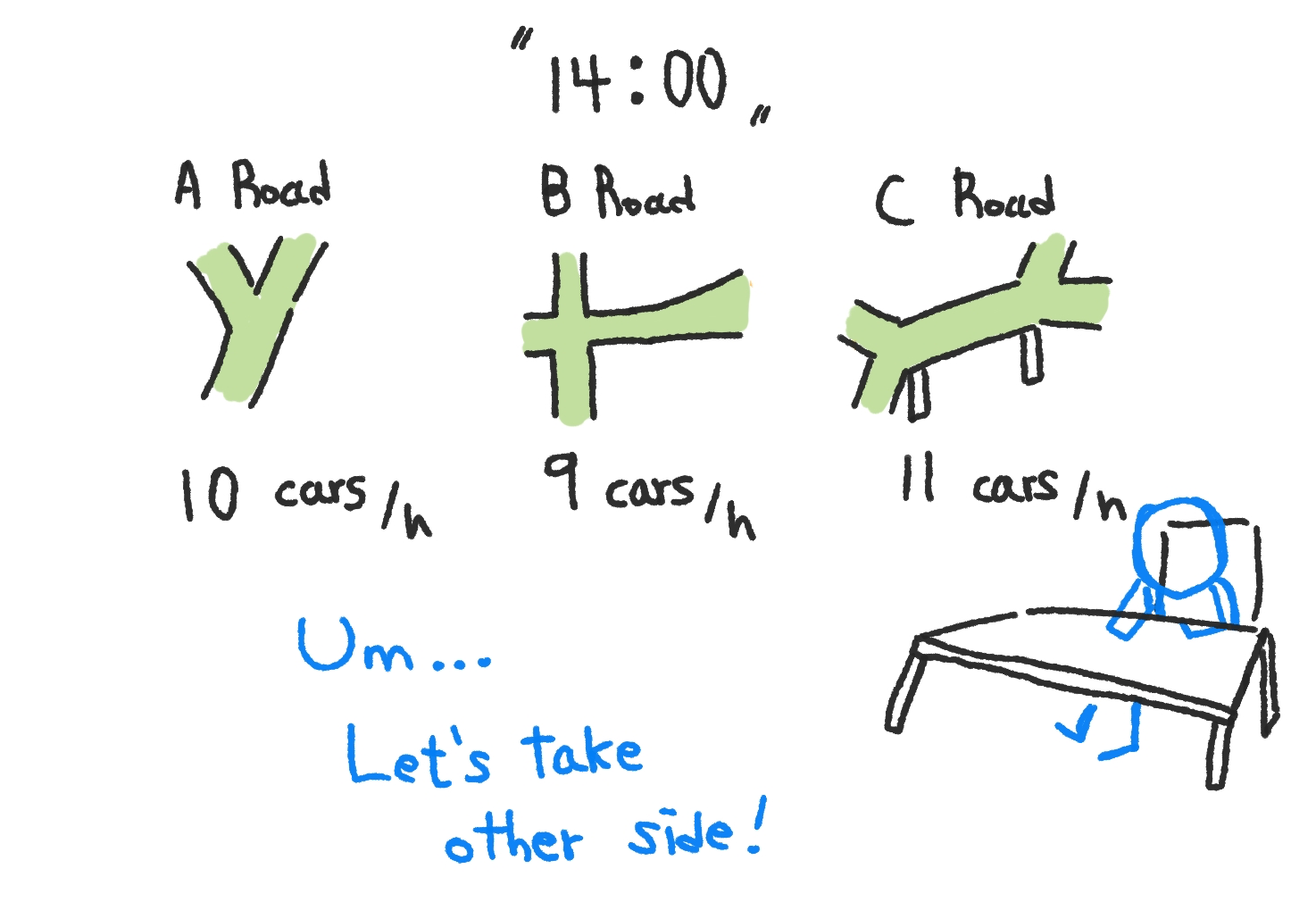
고만고만하니 어떤 길로도 가도 됩니다.
이 경우에 분산이 작지만, 역시 중요한 게 아닙니다.
이 차량 통행량들을 보고,
어떤 길로 가도 괜찮다는 의사 결정을 내린다는 게 중요하죠.
Gaussian Distribution
이제 우리는 분산은 결과를 나타내는 숫자 하나가 아닌
분산을 구하는 과정에 있는 숫자들을 모두 이해할 필요가 있다고 느낍니다.
즉, 분포(distribution)가 중요합니다.
여기서 분포란 어떤 기준에 따라
사건들이 얼마나 발생했는 지 정리해놓은 것입니다.
사실 분포는 어려운 게 아닙니다.
이미 위에서 통행량을 그려놓은 그림도 분포입니다.
즉, 그래프에 선 그려놓는 것만 분포라고 생각하는데 아닙니다.
결국 그래프로 표현하는 게 간단하고 이해하기 쉬울 뿐이지
뭐... 만화나 그림으로 다양하게 표현해서 분포를 잘 설명한다면
당연히 그래프는 버리고 그 방법을 써야겠죠!
가우시안 분포는
우리가 대부분의 현실에서 벌어지는 사건들을
그래프로 그려보니 얼추 다 맞다고 하는 그림입니다.
그 식은 다음과 같습니다.
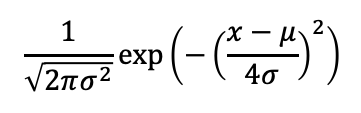
이 함수를 그래프로 그려보면,
(출처 : 위키피디아 - 정규 분포)
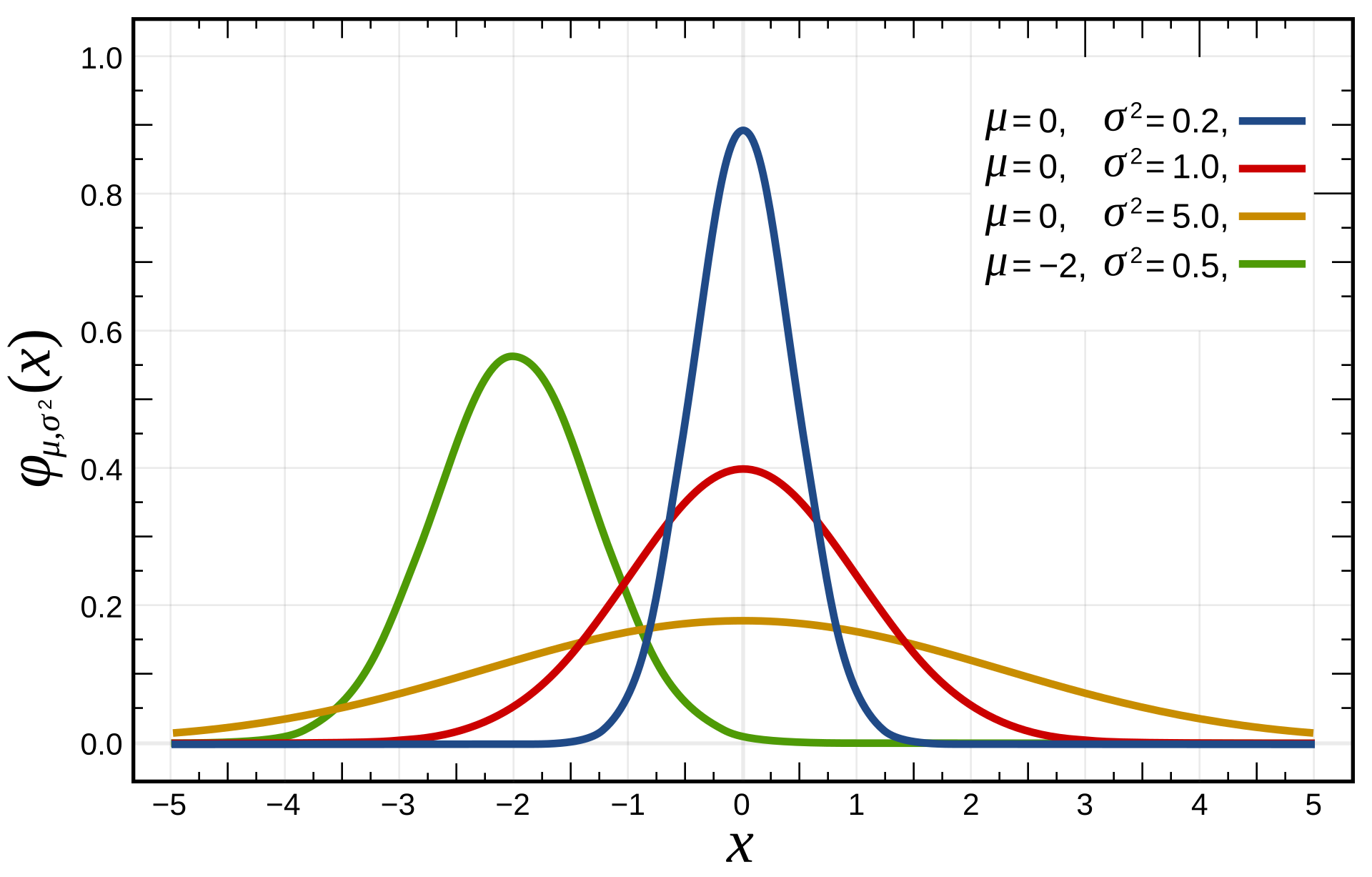
위로 볼록한 모양의 선을 볼 수 있습니다.
u는 평균, o는 표준편차(분산의 제곱근)인데,
여기에 어떤 값을 넣느냐에 따라 볼록한 모양의 위치나 형태가 결정됩니다.
뜬금없이 가우시안 분포?
사실 이걸 왜 알아야 하는지가 중요하죠!
실제로 병무청에서 키를 조사한 결과를 볼까요?
(출처 : 공공데이터포털 - 병무청 병역판정검사 신장 분포 및 청별 현황)

이를 그래프로 그려보면 다음과 같습니다.
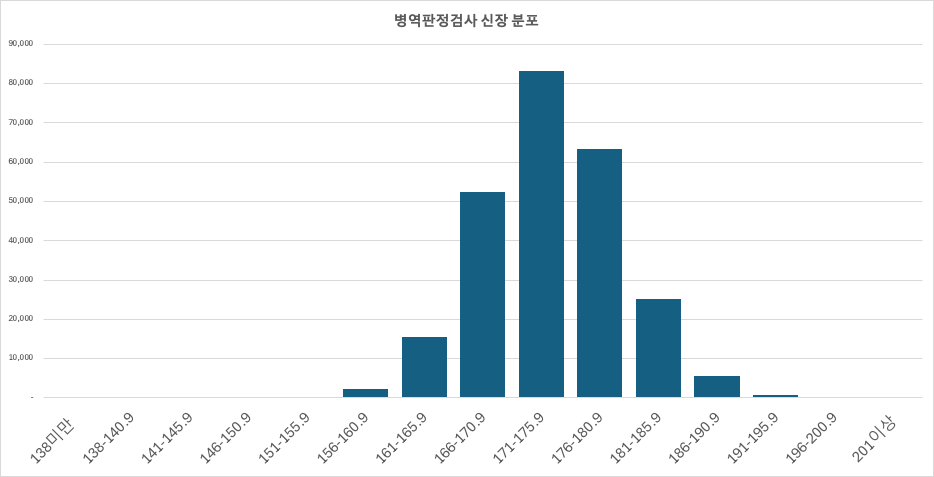
딱 이 모양을 따라서 선 하나 그려보면...
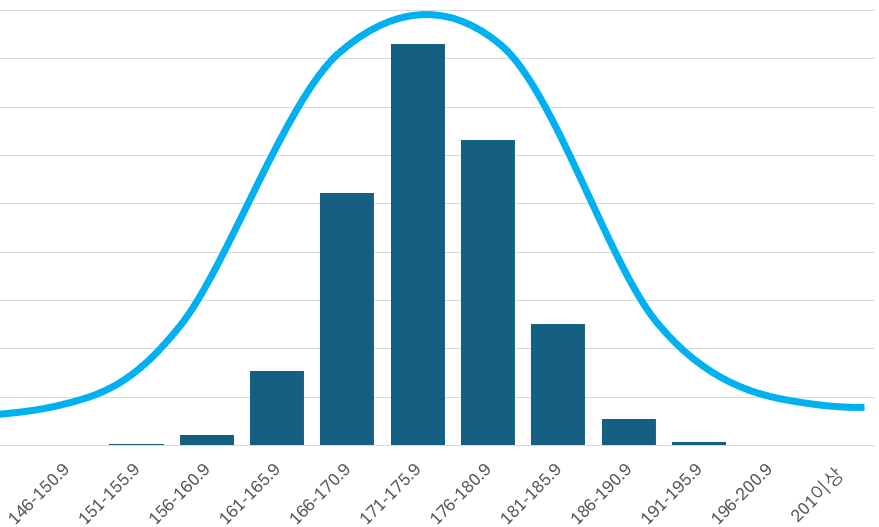
이렇게 위로 볼록한 모양의 선이 등장합니다.
이 선은 바로 가우시안 분포를 그려봤을 때 나오는 모양과 비슷하게 생겼죠.
가우시안 분포는 이렇듯 많은 경우에 있어서
분포를 잘 들어맞게 설명하는 함수를 제공합니다.
그래서 다른 이름으로 정규 분포(normal distribution)라고 부르죠.
이 함수가 없었다면 우린 복잡한 다항식을 머리쥐어 짜내면서 새로 만들어야 합니다.
하지만 반대로 말하면 다른 경우에 있어서도
가우시안 분포를 따라가지 않는 분포가 많습니다.
예를 들어 연도별 출생아 수를 보면,
(출처 : KOSIS 통계놀이터 - 우리나라 출생아 수와 합계 출산율의 변화)
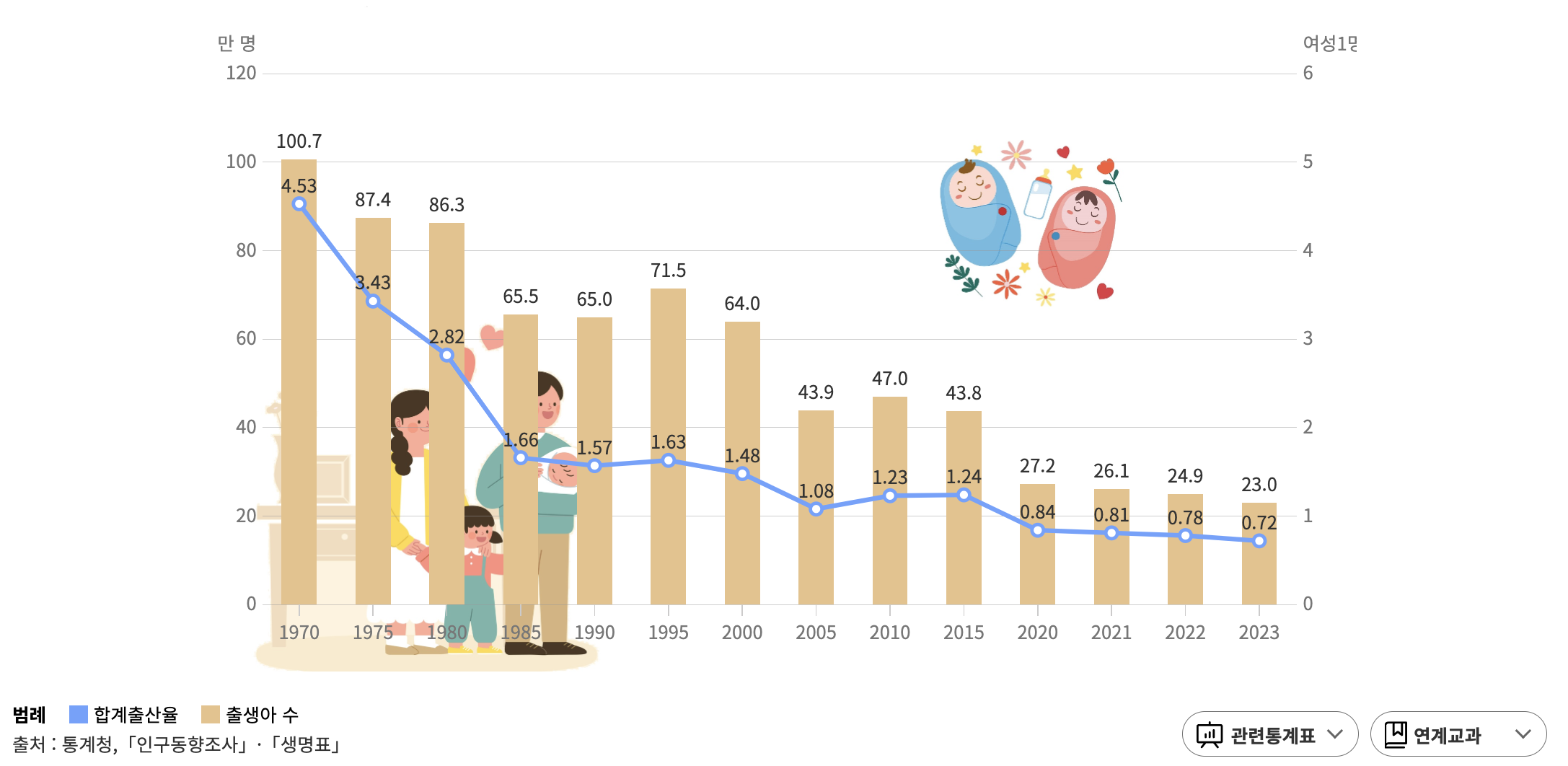
우하향 그래프를 그리죠.
이건 위로 볼록한 모양이 아니니,
이 통계 모델은 가우시안 분포를 적용하기 어렵습니다.
따라서 가우시안 분포는 그 이름과 별개로,
들어맞는 경우가 많았어서 썼을 뿐이지
들어맞지 않는 경우도 있으니
직접 분포를 그려보는 게 가장 중요합니다!
'기계 학습 (Machine Learning) > 수학 (Mathematics)' 카테고리의 다른 글
| 확률과 통계 5 - 자기 정보와 엔트로피 (1) | 2024.08.10 |
|---|---|
| 확률과 통계 3 - 베이즈 정리 (0) | 2024.08.06 |
| 확률과 통계 2 - 조건부 확률 (0) | 2024.08.06 |
| 확률과 통계 1 - 확률 분포 (0) | 2024.08.05 |
| 선형대수 2 - 코사인 유사도와 곱셈 (0) | 2024.08.03 |