2024. 8. 5. 23:01ㆍ기계 학습 (Machine Learning)/수학 (Mathematics)

Probability
1부터 6까지 적혀있는
평범한 주사위를 굴렸을 때,
1일 나올 확률은?
1/6인 건 모두 다 아는 사실이죠.
이렇듯 확률은 우리가 어렸을 때 배웠습니다.
하지만 혹자는 당연히 아는 것에 치우쳐서
확률을 잘 이해하지 못하는 경우가 있습니다.
즉, 주사위는 그냥 당연히 1/6이겠지... 로 생각하는 것이죠.
만일 6을 1로 대체하고, 다시 굴리면 어떻게 될까요?
아직도 1/6일까요?
확률을 계산하는 방법은 간단합니다.
경우(case)의 수와 사건(event)의 수만 알 면 되죠.
경우의 수는 발생 가능한 모든 사건의 개수입니다.
예를 들어 평범한 주사위를 굴리면 나올 눈금은 1, 2, 3, 4, 5, 6이죠.
그래서 경우의 수는 6입니다.
여기서 내가 궁금한 사건을 정하고 개수를 셉니다.
예를 들어 문제에서 1을 말했으니,
저 경우의 수에서 1의 개수를 세면 되죠.
그래서 사건의 수는 1입니다.
그래서 1이 나올 확률이 1/6인 것이죠.
더 나아가 윷놀이를 한 번 생각해봅시다.
윷을 던졌을 때 나올 경우의 수는 총 16개로 다음과 같습니다.

걸이 6개 있네요.
그래서 걸이 나올 확률은 6/16입니다.
필자가 처음 확률을 접했을 때는
윷놀이의 경우의 수는 2의 4 제곱이라고 배웠습니다.
그리고 그 해 확률 관련 수학 문제는 동전 던지기 빼곤 다 틀렸죠.
확률을 못하는 사람의 특징은
그저 숫자만 외울 뿐,
윷을 세는 법을 모르는 것입니다.
이 간단한 이치는 시간이 흘러 어느 인강을 듣고 알았죠.
그 후 확률 문제는 다 맞췄습니다.
사실 다 떠나서, 잘 세기만 해도 확률은 누워서 껌먹기 입니다.
Probability Distribution
확률 분포는 사건에 대한 확률을 모두 구하면 됩니다.
여기서 확률 변수라는 개념이 등장하는데,
어렵게 생각할 필요 없이 조합을 떠올리면 됩니다.
가령 윷 4개를 던져서 나올 수 있는 윷 조합은?
도, 개, 걸, 윷, 모 이죠.
이게 확률 변수입니다.
따라서 윷놀이의 확률 분포는
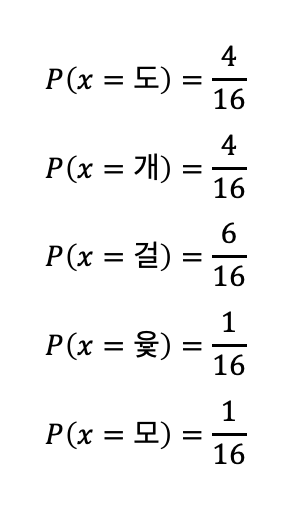
입니다.
잘 보면 함수꼴로 표현된 걸 알 수 있죠?
일반적으로 확률 함수는 P로 표현합니다.
P(x=도)라고 하면 '도가 나올 확률'이라고 생각하면 됩니다.
Probability Mass Function
확률 질량 함수는 설명할 필요도 없습니다.
그냥 위에서 구한 확률 분포를
그래프에 잘 그려주면 됩니다.
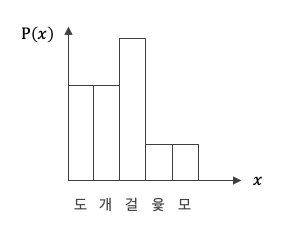
너무 쉽죠?
'기계 학습 (Machine Learning) > 수학 (Mathematics)' 카테고리의 다른 글
| 확률과 통계 3 - 베이즈 정리 (0) | 2024.08.06 |
|---|---|
| 확률과 통계 2 - 조건부 확률 (0) | 2024.08.06 |
| 선형대수 2 - 코사인 유사도와 곱셈 (0) | 2024.08.03 |
| 선형대수 1 - 벡터와 행렬 (0) | 2024.08.02 |
| 기계 학습을 위한 수학 개요 (0) | 2024.08.02 |